Bewegungen von zwei sich gravitativ beeinflussenden Himmelskörpern sind in der Regel mathematisch relativ genau berechenbar. Erhöht man die zu beachtende Anzahl an Objekten jedoch auf drei oder mehr, so steht man vor einem unlösbar erscheinenden Problem: dem Dreikörperproblem, auch bekannt als Mehrkörperproblem. Für die Bahnen von den Himmelskörpern gibt es in diesem Fall keine Lösungen mehr, die sich mit herkömmlicher Mathematik berechnen ließen und man kann lediglich versuchen, sich durch numerische Computerberechnungen den Lösungen anzunähern.
Um es einfacher zu halten, wird das Dreikörperproblem in der Praxis oftmals als eingeschränktes Dreikörperproblem behandelt. Was die Erde betrifft, ist das eingeschränkte Dreikörperproblem von erheblicher Bedeutung. Will man beispielsweise eine Sonde in den Weltraum schicken, ist diese dort der Anziehung etlicher Himmelskörper ausgesetzt, allen voran der Erde und der Sonne. Die anderen Planeten des Sonnensystems sind in diesem Fall aufgrund ihrer Entfernung und der daraus resultierenden (relativ gesehen) schwachen Anziehungskraft nicht ausschlaggebend. Die Sonde als solche ist in diesem Problem vernachlässigbar, da ihre Masse verglichen mit der Masse der Sonne bzw. der Erde extrem gering ist. Mithilfe der Vereinfachung des Dreikörperproblems zu einem eingeschränkten Dreikörperproblem können nun näherungsweise Lösungen für stabile Umlaufbahnen berechnet werden. Daraus ergeben sich die sogenannten Lagrange-Punkte, an denen sich die eigentlich wirkenden Kräfte gegenseitig aufheben. Der masseärmste Körper (Sonde) bewegt sich dabei mit der gleichen Umlaufzeit wie der zweitschwerste Körper (Erde) des Systems um den Massenmittelpunkt, welcher in diesem Beispiel sehr nahe bei der Sonne liegt. In einem System zweier Himmelskörper gibt es fünf dieser Lagrange-Punkte (abgekürzt L1-L5).
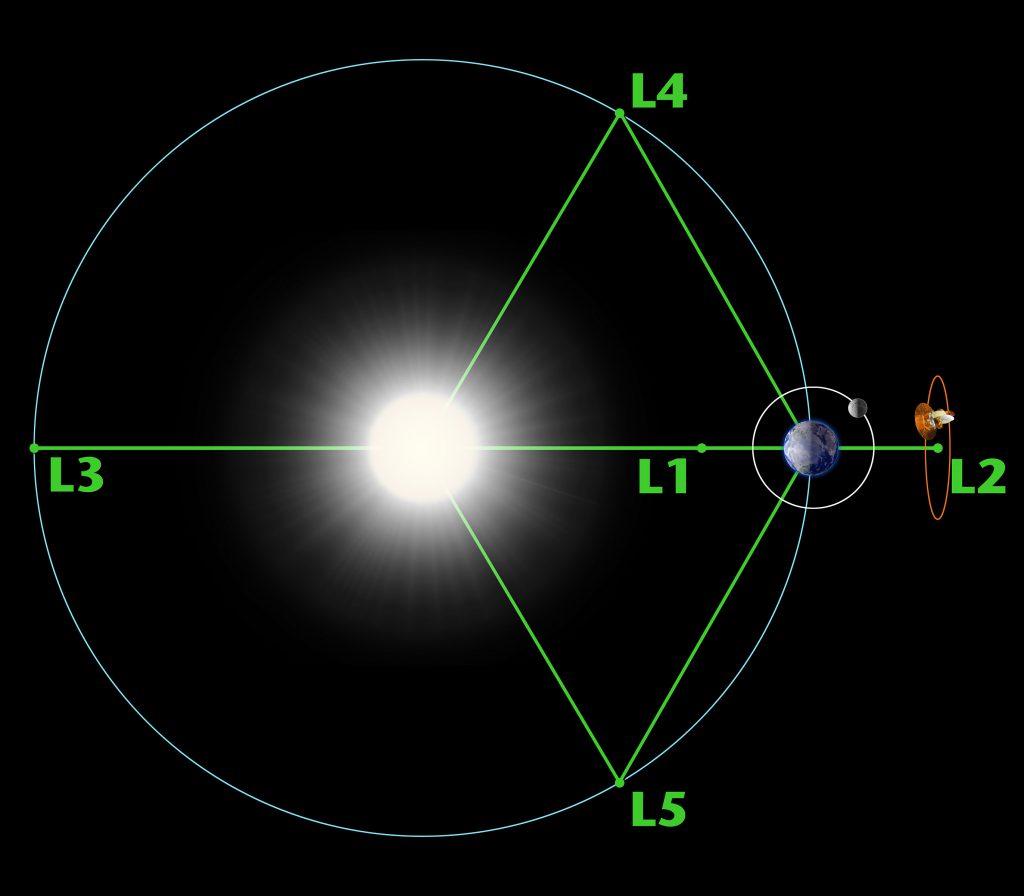
© NASA/WMAP Science Team
https://solarsystem.nasa.gov/system/resources/detail_files/754_990528.jpg
Zu beachten ist, dass sich die Lagrange-Punkte in ihrer Stabilität unterscheiden. L1, L2 und L3 sind insgesamt instabil, das heißt, nach einiger Zeit müssten Bahnkorrekturen durchgeführt werden, um die Sonde dauerhaft am jeweiligen Lagrange-Punkt zu halten. L4 und L5 sind hingegen langfristig gesehen stabil. Für die Forschung bieten die einzelnen Lagrange-Punkte unterschiedliche Vorteile. L2 eignet sich beispielsweise hervorragend zur Stationierung von Weltraumteleskopen, da die Gefahr, welche von der Sonnenstrahlung ausgeht, dort wesentlich geringer ist als an den anderen Lagrange-Punkten. Momentan befinden sich an L2 unter anderem das Herschel-Teleskop, das Planck-Teleskop und die Raumsonde Gaia. Auch das James-Webb-Teleskop, der Nachfolger des weltberühmten Hubble-Teleskops, soll an diesem Lagrange-Punkt stationiert werden. An L4, einem der stabilen Lagrange-Punkte, wird die Erde von einem Asteroiden besonderer Art um die Sonne begleitet: einem sogenannten Trojaner, welcher den unspektakulären Namen 2010 TK7 trägt. Als Trojaner werden in der Astronomie alle Asteroiden bezeichnet, die sich an den Lagrange-Punkten L4 oder L5 auf der Umlaufbahn eines Planeten um die Sonne aufhalten. Der Erdtrojaner wurde 2010 erstmals entdeckt und ein Jahr später bestätigt. Seine physikalischen Eigenschaften sind allerdings nur teilweise bekannt. Nachdem die Helligkeit 2010 TK7s gemessen wurde, konnte man daraus eine Größe von etwa 300 Metern ableiten. Für einen erdnahen Asteroiden wäre dies relativ groß. Er wird uns in absehbarer Zukunft jedoch nicht gefährlich werden, da seine Bahn erst einmal stabil ist und 2010 TK7 an seinem Lagrange-Punkt „gefangen“ gehalten wird.





Neueste Kommentare